A look into composing, Composability, Immutability

August 2019 · 12 minute read

An ordinary work day,
I’m adding a feature to our JavaScript driven tables so it can pull/push data while navigating between the pages(I belive in common tongue they call this "pagination"). I wrote two functions named retrieveItems and drawItems. As I’m building the retrieveItemsAndDraw function, this is what I find myself writing:

const retrieveAndDrawItems = R.compose(drawItems, retrieveItems)

At that time one of the guys in my team creep up behind me and ask what I’m up to, and what that line does. "Simple!" I answer, "It’s just myCompose = fs ⇒ x0 ⇒ fs.reverse().reduce((x, f) ⇒ f(x), x0)~".

But that answer isn’t correct. And compose (or function composition) as simple as it may be is a fundamental concept and need to be understood and explained properly. This text has been written for the sake of myCompose; to understand it and to explain it in detail.

Composing functions

Do you remember function composition from mathematics? It’s when you join multiple functions together to create a new one. Joining, or compose or composability is the bread and butter of functional programming in achieving modularity.

f,g,fog
f(x) = x + 2
g(x) = x * 3
(fog)(x) = f(g(x)) = (3 * x) + 2
f,g,fog JavaScript’te
f = x => x + 2
g = x => x * 3
fog = x => f(g(x))

Building the compose function

My next step is to write a generic compose function; a function that takes two functions and joins them; but first I would like to be able to describe the inputs and outputs of those functions so I can argue about how they can be joined together.

In functional languages, function signatures resemble that of Haskell:

  1. string → int : A function. Takes string and returns int

  2. f :: string → int: The function named f takes string and returns int

  3. int → int → int: A function that takes 2 integers and returns one integer

  4. indexOf: [string] → int: a function named indexOf that takes string list and returns an int

  5. find :: ['a] → Maybe 'a: a function that takes a list of a generic type(a), and returns a Maybe container with a value of that same type (a) in it

Being able to read function signatures will help me argue about which functions I can compose together and how. Lets return to a a simple composition example to see how:

f,g,fog in JavaScript
f = x => x + 2
g = x => x * 3
fog = x => f(g(x))

If I know what type inputs and outputs f and g have, then I can know what their composition will input and output:

f :: 'a -> 'b
g :: 'b -> 'c
fog :: 'a -> 'c

Or to give more concrete examples:

//myParseInt :: string -> int
myParseInt = parseInt (1)

//indexOf :: 'a -> ['a] -> int
indexOf = x => xs => xs.indexOf(x)

//increment :: int -> int
increment = x => x + 1

//uppercase :: string -> string
uppercase = x => x.toUpperCase()

// cities :: [string]
cities = ["ANKARA", "ISTANBUL", "KAYSERI"]

// indexOfCity :: string -> int
indexOfCity = x => indexOf(uppercase(x)) (2)
1 parseInt would return NaN for things that it cannot parse into numbers, but lets ignore that for the moment
2 the function indexOfCity is indexOf and uppercase put together. As in the case of (fog)(x) but with indexOf in the place of f , uppercase in the place of g.

Similarly, we can see uppercase(myParseInt("4")) is faulty but increment(myParseInt("4")) is not.

As I said, splitting a problem into functions and creating solutions that are composed of those functions is the basic functional approach to programming. Which is why in Haskell to compose two functions into one is as easy as typing .:

composing in Haskell
indexOfCity = (indexOf . uppercase)

In JavaScript however we have to roll our own:

f,g,fog in JavaScript
//compose :: (('b -> 'c), ('a -> 'b)) -> 'a -> 'c  (1)
compose = (f, g) => x => f(g(x))

f = x + 2
g = x * 3
fog = compose(f, g)
1 If that is looking complicated I suggest you pause and wait till it clicks until you proceed further

In fact, if I did the same in OCaml and queried the type of compose I would get:

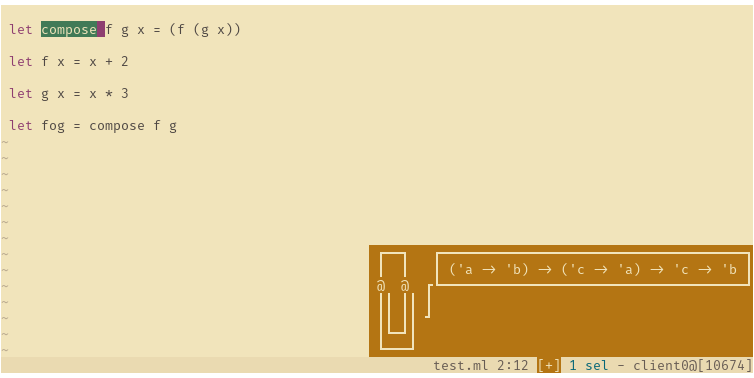
OCaml compose

In OCaml to call a function named f with the arguments x and y, instead of the familiar f(x, y) we say f x y.

Operators like + and - come between its two arguments, as in x + 2. We can create infix methods (like a + b) as well as prefix ones (like (+) a b) if we desired:

let (><) f g x = f (g x)
let f x = x + 2
let g x = x * 3
let fog = f >< g

But in OCaml the pipe operator (|>) is preferred to compose:

let fog x = x |> g |> f

There is also a proposition to have the |> operator added to ECMA
In Kakoune, the command :lsp-hover can show me the signature of whatever my cursor is on

A general purpose compose method

Sometimes I feel like composing more than two functions together. In JavaScript this is also trivial to accomplish:

an innocent piece of code that tries to compose functions
compose = fs => x0 => (fs (1)
                        .reverse() (2)
                        .reduce((x, f) => f(x), x0)
                      )
1 I could have got variable number of arguments instead of an array by declaring the function as compose = (…​fs) ⇒ …​
2 Because compose([f, g])(x) means f(g(x)) , not g(f(x)) ; I reverse the list. reduce would iterate over the list from the beginning to the end.

Did anyone else have their spider senses tingling after reading the compose function above?

The compose above DOES NOT WORK

But why does it not work?

const f = x => x + 2
const g = x => x * 3
const h = x => x * x

const hfg = compose([h, f, g])

hfg(5) // 289
hfg(5) // 81
hfg(5) // 289
hfg(5) // 81
//And it continues forever in the same pattern

Have you realized that hfg does h(g(f(x))) first, and f(g(h(x))) after?

Immutability

const f = x => x + 2
const g = x => x * 3
const h = x => x * x

const funs = [h, f, g]
const hfg = compose(funs)

hfg(5) //result 289
console.log(funs) // [ [Function: g], [Function: f], [Function: h] ]
hfg(5) //result 81
console.log(funs) // [ [Function: h], [Function: f], [Function: g] ]
hfg(5) //result 289

Is it obvious yet?

The reverse method of Array modifies the array it is called on.
So it turns out reverse is mutative.

Mutative Function

Mutative function simply does what its name suggests; it may mutate the program state

To get into what state is I believe it’s best to know what a pure function is.

In Ruby the mutative functions have a ! at the end of their names. If a function is named reverse! instead of reverse you very well know that it modifies something somewhere.

Pure Function

In mathematics (if you remember) a function is just a relation between two sets.

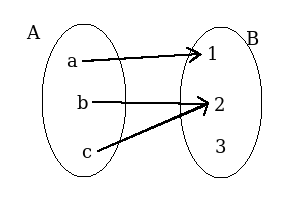
function diagram
eg.a function from A to B

Lets call this function fab and write it in JavaScript:

const A2B = { a: 1, b: 2, c: 2 }
fab = x => A2B[x]

Like how fab maps A to B, f(x) = 2x + 3 is a function that maps natural numbers to natural numbers.

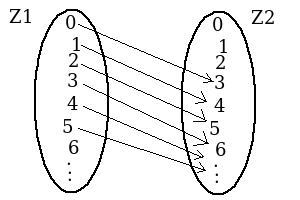
function diagram
eg:f(x) = 2x + 3 function mapping Z to Z

Functions like fab and f(x) = 2x + 3 that only map one set to the other are called pure . The definition pure function may make more sense knowing what a side effect is:

Side Effect

Lets say our fab method does not only map A to B, it does more; it renders a text in a webpage:

fabAndEdit = x => {
	document.querySelector("#text").innerHTML = x
	return A2B[x]
}
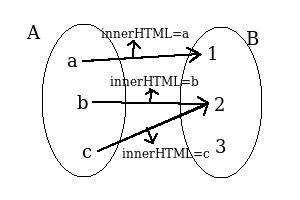
function diagram with side effects
eg:fabAndEdit

Like the setting of innerHTML, any effect that is not a mapping of an input to an output is called a side effect.

You can also think of a side effect as anything that changes the program state.

State is the state of a program or a computer. For example when you press a button on your keyboard, you change the state of your computer from a computer to a computer-that-has-a-button-pressed. If you modify a textbox the state of the program is changed, something writes in that textbox that didn’t write before; if a different piece of code were to read the value of that textbox after it has been modified it will find a different value than it would before.

  • Functions that don’t modify the state are called pure functions.

  • If a function is modifying the state that modification is called a side effect.

  • Pure functions don’t have side effects. Functions that have side effects are not pure.

  • Pure functions always give the same result for the same input no matter when they are called.

  • Mutative functions have side effects. Mutative functions are not pure.

The Mental Overhead of Mutative Functions

The number of objects an average human can hold in working memory is 7±2

— George A. Miller
The Magical Number Seven

Our mental capacity is not limitless; and if you are like me you’re listening to a podcast with one ear, while the other ear is focused on the sounds coming from the meeting room to check if anyone is saying anything about you; while you’re writing code.

In addition for every function in your code, instead of having to ponder if and how they’re modifying the program state, how they’re modifying the global variables, if they overwrote your function arguments; if you wrote them pure, if you limited their side effects (if any) it would make your code more maintainable (then again, there is no program that doesn’t have side effects; what’s the point of a program if it doesn’t take an input and it doesn’t produce an output. We could even get philosophical and argue that if we can’t see the output of a program, it does not exist).

Side effects can be purified by making them lazy.

Let me explain what that means…​

If a function doesn’t produce its output immediately, if the result is delayed until the moment it is needed that function is called lazy.

Haskell, for example, is an inherently lazy language. In OCaml we can have lazy values by declaring them lazy. In JavaScript (as usual) we have to hack our own:

counter = 0

incrCounter_unsafe = () => {counter ++}
incrCounter = () => () => {counter ++}

range = n => { let l = []
               for (let i = 0; i < n; i ++) { l.push(i) }
               return l }

range(3) (1)
console.log(counter) (2)
range(3).forEach(incrCounter_unsafe)
console.log(counter) (3)

counter = 0
lazyFuns = range(4).map(incrCounter)
console.log(counter) (4)
lazyFuns.forEach(f => f())
console.log(counter) (5)
1 [0, 1, 2]
2 prints 0
3 prints 3
4 prints 0
5 prints 4

incrCounter_unsafe is impure, because it modifies the global variable counter. incrCounter_unsafe upon being called does what it must: it immediately changes the value of counter.

On the other hand incrCounter function doesn’t do a thing when it is called, it just says "hey man…​ I really can’t be bothered right now. Here just take this and you just call it yourself, won’t you?" returning a function. No change happens in the program state until the returned function is called; which is why incrCounter is safe and lazy.

An all-purpose solution for things lazy would be:

class LazyF {
	constructor(f)   { this.$f = f }
	// map :: LazyF ('a -> 'b) -> ('b -> 'c) -> LazyF ('a -> 'c)
	map(f) 	     { return new LazyF(x => f(this.$f(x))) }
	// chain :: LazyF ('a -> 'b) -> LazyF ('b -> 'c) -> LazyF ('a -> 'c)
	chain(o) 	     { return new LazyF(x => o.performUnsafe(this.$f(x))) }
	// performUnsafe :: LazyF ('a -> 'b) -> 'a -> 'b
	performUnsafe(x) { return this.$f(x) }
}

foo = x => {console.log("x: " + x)
            return x + 1}
foo(5) (1)
new LazyF(foo) (2)
new LazyF(foo).performUnsafe(5) (3)
new LazyF(foo).map(foo).performUnsafe(5) (4)

counter = 0
//incrCounter :: () -> LazyF (() -> ())
incrCounter = () => new LazyF(() => {counter ++})
lazy = (incrCounter()
          .chain(incrCounter())
          .chain(incrCounter()))
console.log(counter) (5)
lazy.performUnsafe()
console.log(counter) (6)
1 prints x: 5 and returns 6
2 LazyF {'$f': [Function: foo]}
3 prints x: 5 and returns 6
4 prints x: 5 and x: 6 , returns 7
5 prints 0
6 prints 3
Haskell can be a purely functional programming language by wrapping every side effect in containers called IO
A similar solution to LazyF can be found in a JavaScript library named crocks , under a different name: Arrow

Mutability, Immutability

A term that goes hand-in-hand with "mutative". Compare the behaviour of the Array in JavaScript to that of ImmutableArray

While push method of Array modifies values, the push method in ImmutableArray doesn’t. Data types like ImmutableArray that protect their states are called immutable. Immutable values also encourage purification of the functions they are used in

In functional languages you don’t have to struggle to achieve immutable values; they are supported natively.

For example in OCaml the concept of variable doesn’t exist. To think about it the name "variable" in mathematics actually contradicts with what it actually is; you can’t declare g = 9.8 in the beginning of your formula and half way through change g to something else; if a variable doesn’t vary, then it isn’t a variable is it?

In OCaml once you say let a = 5 , a is always a label for the value 5. If you want modifiable values you could let counter = ref 5 and then counter ← !counter + 1.

For records:

ocaml mutable records
type sex = Male | Female
type person = {name: string;
               age: int;
               sex: sex;
              }

let a_person = {name="Bruce"; age=60; gender=Male}
a_person.sex <- Female (* ERROR *)

let a_new_person = {a_person with name="Caitlynn"; gender=Female} (* OK *)

type changable_person = {mutable name: string;
                         age: int;
                         mutable sex: sex;
                        }
let a_person2 = {name="Bruce"; age=60; gender=Male}
a_person2.name <- "Caitlynn"
a_new_person <- Female

If you too want to write code with immutable values but having your JavaScript focused team switch to OCaml is out of the picture, you may want to try immutableJS: a library that provides immutable implementations of many collection data types

If your answer is "thanks but no thanks" then I can only wish you luck with your endless clone()ing and slice(0)ing…​

Uhm, Conclusion?

In conclusion we have a working compose method:

compose
reverseList = l => l.slice().reverse()

compose = (...fs) => x0 => reverseList(fs).reduce((x, f) => f(x), x0)

Of course the kid that asked me what R.compose does has long gone…​ He didn’t stick around to listet to my storytelling. That’s OK though, I’ll mansplain to him tomorrow continuing from where we left off…​